Ganita Sutras
Ganita Sutras is a complete system in itself. These are Vedic aphorisms. These
are 29 in number; 16 of them are designated as Sutras and other 13 as Upsutras.
Credit goes to Swami Bharti Krisna Tirthaji Maharaj, a Shankracharya of
Kanshipeeth to focus the attention of the present generation about
potentialities of Sutras.
The information contained in the book titled "Vedic Mathematics" compiled by
Prof. V.S. Agarwala, published (1965) from the manuscript papers of Swamiji make
us known as how Swamiji had to devote many years to decode the working rules of
these Sutras.
From the demonstrations of the working rules of these Sutras in this book it has
convinced many about the potentialities of the Sutras. Since then many scholars
have further demonstrated about their potentialities to make the mathematics
much easier and more effectively within the comprehensions of much larger
population and also about their utility and academic values in many ways. Dr. S.
K. Kapoor has approached the organization format of this system on the whole and
as individual Sutras. His approach and the results give us further insight of
this wonderful system.
Here Sutras 1, 2 & 3 and Upsutras 1 & 2 are being introduced from the book
"Goldbach Theorem" to give insight about their formats and to give idea about
the basics of the different processes and the way this system is approaching
different branches of mathematics in a unified way as a single discipline. The
parallel text of the Sutras adopted in different scriptures is being searched.
Dr. Kapoor points out Shatpath Brahman. Hereunder, the illustrative reference
with working rule is indicated in reference to Ganita Sutra 1. The other Sutras
may be taken up in due course of time.
GANITA SUTRA 1
Text in Roman script:
Ekadhikena Purvena
Working rule / simple English rendering:
“One more than the previous one.”
Source concept:
“One”
Format:
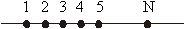
Basics / technical words:
Text avails three technical words which take us to the basics of the working
domain of the Sutra. These are: (1) Eka (one), (2) Edhikena (more than), and (3)
Purvena (previous). These three technical words take us to the three basic
concepts: (1) the concept of “one”, (2) the concept of “one more than”, and (3)
the concept of “previous one”. The first concept is the wholesome concept. Here
it manifests in many ways and can be availed as a unit, unit entity, unit
measure, the counting number 1, the close interval of unit length etc. etc. The
second concept “more than” is the concept of increase, the concept of comparison
of one entity being bigger than / more than other entity. The third concept is
the concept of “order”. It is the concept of a queue, a pair of entities of a
queue of which one is previous as comparison to the second and the second
automatically being subsequent to the first. Therefore, the Sutra 1 has many
applied values which would work out for us (1) counting, (2) arrangement of
counting pebbles, (3) arrangement of beads along a thread, (4) the queue of
points along with line etc. etc. If we try to chase the repeated applications of
“one more than the previous one”, we can have a countably infinite steps. Not
only that, we can by a suitable choice of “one” and the application of the
working rule of Sutra 1, have a chase for uncountable infinity as the line is by
having sequential placements of points as counts with index values allotted as
per the working rule of Sutra 1 from the set of natural numbers (whole numbers /
counting numbers).
Parallel text and application of Sutra 1 in Shatpath Brahman:
1.1.2.5 (Kanda 1, Parpathaka 1, Brahmana 2, Kandika 5) Page 10
YADEV AGRE TAD KARVANITE
That which is first to be acted first.
2.5.2.22 (Kanda 2, Parpathaka 5, Brahmana 2, Kandika 22) Page 300
EKAIN EKEIN YA ASYE PRAJA .......... EKE NATI RIKTANI
For everybody there is one utensil. As many are the members of the family,
so many are the utensils and there is one extra.
2.6.2.4 (Kanda 2, Parpathaka 6, Brahmana 2, Kandika 4) Page 328)
EKAIN EKEIN YA ASYE PRAJA .......... EKE NATI RIKTANI
For everybody there is one utensil. As many are the members of the family,
so many are the utensils and there is one extra.
Let there be a family F of members m1, m2, .........mf. Let this family has a
kitchen K with utensils
u1, u2, ..........uk.
For one-to-one association of family members of F with the utensils of K, the
first member m1 is to be associated first, the first utensil of K i.e. u1.
To each member of F is associated from K.
The requirement is that after such association we should have one extra utensil
in K. This makes the cardinality of K as f+1.
The set F (of cardinality f) and the set K (of cardinality f+1) makes a pair of
sets (F, K) and they supply us the pair of numbers (f, f+1). This is precisely
the basics and formation of Ganita Sutra 1.
GANITA UPSUTRA 1
Text in Roman script :
Anurupyena
Working rule / simple English rendering:
“Proportionate selection (of multiples and sub-multiples)” / “proportionately”.
Source concept:
“Oneness” / symmetry
Format:
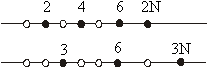
Basics / technical words:
The text of Upsutra 1 avails a pair of technical words: (1) Anu (to follow), and
(2) Rupyena (the form of). When ‘one’ is viewed as synthetic i.e. composed of
parts, then each of its parts would be symmetrical to the whole and it would be
proportionate of the whole. As such, (1) part as symmetrical to the whole, and
(2) part as proportionate of the whole would be two distinct aspects of the same
organisation. Infinity is another word in which melt away all finiteness. In
infinite domains or self-contained domains, the uniformity and patterns are
other keywords in terms of which the concept of oneness can be approached as a
symmetry and proportions. The applied values of Upsutra 1 would help us reach at
unit interval as replica of infinite line, the universality of Yatha pinde tatha
brahmande (as in the body so in the universe) and Yatha brahmande tatha binde
(as in the universe so in the body) as well as the universality of the
Upanishadic comprehensions as that even when full is taken out of full, there
still remains full. With this, when one would work Sutra 1 with double of a unit
instead of a unit or with any multiple of a unit instead of a unit, one would
see that the rule works. With this, the Sutra 1 coupled with Upsutra 1 makes the
potentialities of Sutra 1 manyfold.
GANITA SUTRA 2
Text in Roman script :
Nikhilam Navatascaramam Dastah
Working rule / simple English rendering:
“All from nine and last from ten.”
Source concept:
Ten place value system is the source concept.
Format:
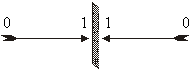
Basics / technical words:
Text avails four technical words which take us to the basics of the working
domain of the Sutra. These are: (1) Nikhilam (all), (2) Navastasca (from nine),
(3) Caramam (last), and (4) Dastah (ten).
Nine numerals and ten place value system are the two basic steps in terms of
which the infinitely long line stands tamed. The counting pebbles technique
requires infinite pebbles for coverage of infinitely long line. However,
symmetry / proportions / replica rules suggest that proper system can be
constructed to express “infinity in terms of finite”. Vedic seers comprehended
ten place value system. From the method of expression tenth counting pebble as
10 as in two digit form, we can notice that here lies a shift from single digit
expression for first 9 counts to the next multiple digit expression initiation
for expression of tenth count onwards. We also know that first 9 counts as well
can be expressed in double digit forms as: 01, 02, 03, 04, 05, 06, 07, 08 & 09.
Therefore, the first thing about this transition is the introduction of the
tenth symbol for the zero count as “0”. Further, it also would be interesting to
note that the double digit form for 1 as 01 provides us an expression for the
tenth count as 10 simply by having swapping of places for first and the second
digit. Further, the above interlink of 01 and 10 takes us to their link and
inerlocking as reflection pair of numbers as much as that the formats beneath 01
and 10 get interconnected like image of an arrow through looking mirror gets
interlocked with the arrow itself. The placements of arrow, mirror, and the
image of the arrow work out a di-monad format with mirror playing the role of
joint of the di-monad. This as such is a big leap forward from the organisation
format of Sutra 1. This had become possible with the transition stage of Upsutra
1. Therefore, Sutra 1, Upsutra 1 and Sutra 2 together make much interesting
dimensions to the mathematics.
The above organisation of Sutra 1, Upsutra 1 and Sutra 2 takes us to a stage
where the middle of interval, which otherwise had the privilege of uncountably
infinite placements, gets tamed as a unique mirror placement to have half unit
in front of the mirror as first half and its image through the mirror as the
second half. It is this way unique fixation of the middle makes the mathematics
workable in terms of “half unit”, like the organisation in terms of “half
dimension”. With this, it becomes possible to go to a number which exists prior
to “one” i.e. half. It is a big achievement over the mathematics of “one”
without predecessor. However, simultaneously, it makes the working very delicate
as we shall be permitting the second half to remain dormant while structures
because of the second half also shall be silently marking their presence. We
cannot afford to ignore the existence of the structures because of the second
dormant half. If one is to see the type of difficulties in which the mathematics
when worked without taking care for the second dormant half, one is simply to
pose to oneself as to why from hypercircle-8 onwards the values start
decreasing. It simply happens as the linear order worked in terms of
half-dimension helps us sequentially increase only uptil seventh step parallel
to the possible seven geometries of 3-space of linear order.
The organisation of pairing of two halves with the help of a mirror at the
middle is unique organisation of many features, of which the most important is
the feature of common remainder for both the halves while both halves are
divided by a common divisor. Though this property may appear to be obvious but
in fact when the same is viewed in the context of uncountably infinite points
being handled in terms of counting numbers, one would realise, how important
this property of constant remainders emerges to be. This is precisely Upsutra 2.
GANITA UPSUTRA 2
Text in Roman script :
Sisyate Sesasmajnah
Working rule / simple English rendering:
“Remainder remains constant.”
Source concept:
The source concept here is the concept of equality of units, the pair of halves
etc. etc.
Format:
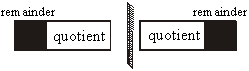
Basics / technical words:
The basic / technical word availed by the text of Upsutra 2 is “Sesa”
(remainder). The text as such is the definition of remainder: remainder is that
which remains (as uncovered part of the divisor, on division).
The basic operation is the operation of “division”. This Upsutra along with
Upsutra 1 makes the mathematics of Upsutras a very interesting branch in itself.
The “one” which permitted itself as a pair of halves, sequentially by the rule
of symmetry of Upsutra 1 and the rule of equality of remainders of division of
equals takes the process of partitioning of “one” into as many equal parts as
one would like to have.
This makes the external expansion of counts from one to two, two to three and so
on parallel to the internal partitioning from wholesome one to a pair of parts,
then to three parts, four parts and so on. With this, the arrays of mathematical
tools become sufficiently large to work out very rich structures only in terms
of “parts”, of which the working with “half” is most rewarding.
GANITA SUTRA 3
Roman script :
Urdhva-Tiryagbhyam
Working rule / simple English rendering:
“Vertically and crosswise.”
Source concept:
The source concept is the partitioning parallel to reflection pairing of object
and image.
Format:
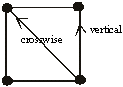
Basics /
technical words:
The basic / technical words availed by the text are: (1) Urdhva (vertical) and
(2) Tiryag (crosswise).
We may illustrate one of the working rules of this Sutra, which would help us to
reach at its organisational format as well. Let us multiply 11 by 11. We shall
be getting the product equal to 121. Let us have a close look at this number.
The central digit of this number is 2. It admits expression as 1+1. Let us
replace the central digit 2 with its above expression 1+1. The three parts of
the number 121 would permit depiction as: 1, 1+1, 1. Now, let us chase the
multiplication the Sutra way:
The first Sutra gives us the working rule to proceed step by step as “one more
than the previous one”. When we are working only with “half”, therefore, in this
case of 121 we shall be requiring the last two digits 12 or the first two digits
21. Therefore, when we shall be having 1 as start with position, as a next step
under the rule of Sutra 1, we shall be reaching at 12. Then the reflection image
of 12 would give us 21 and we shall be obtaining 121. If we would have been
multiplying 111×111, we would be obtaining in three steps 123 and its image 321
which when combined would give us 12321 as the product of 111×111. Likewise if
we would have been multiplying 1111×1111, we would be obtaining in four steps
1234 and its image 4321 which when combined would give us the required product
as 1234321. The process can be extended.
The product 11×11 being the product of pair of numbers of double digits,
therefore, these four digits, here each being 1, can be expressed as the numbers
located at the four corners of a square. The pair of above corners may be taken
as representing the first number 11 and the pair of lower corners may be taken
as second number 11.
Now, when we shall be multiplying the first digit of lower number 11 with the
pair of digits of the above number 11 one by one, we shall be approaching as is
depicted above in terms of the arrows.
The depiction is of two parts. The first part is Urdhva (vertical) and the
second part is Tiryag (crosswise). This as such, would help us comprehend as
that geometric format of square is being divided into two triangles and only 1
out of two triangles is being utilised by the organisation format of Sutra 3.
Here it would be relevant to note that the triangle is the first close
organisation of lines. In other words we require a minimum of three lines to
have a close organisation to enclose planes (area) / surface within its lines.
The triangle as such is the printout of 3-space on 2-space. The sum of all the
three internal angles of a triangle isp. The sum of all the three external
angles of a triangle is 2p. We can express p as (3–2)p. The sum of all the four
internal angles of a quadrilateral is 2p. We can express it as (4–2)p. In
general, the printout of n-space on 2-space is n-polygon and the sum of the
internal angles n-polygon is (n–2)p. This in general can be seen as that the
printouts of n-space in the role of dimension on 2-space is n-polygon.
Therefore, the organisation format of Sutra 3 is that of a printout of 3-space
in the role of dimension on 2-space format.
Like that, one can proceed to reach at the organisation formats of the entire
range of the text of 16 Ganita Sutras and 13 Upsutras but the context and the
space at hand would not permit to proceed ahead with it.
However, the organisation formats achieved uptil this stage well indicate about
the mathematics of linear order of Sutra 1, spatial order of Sutra 2 and of
solid order of Sutra 3.